A 20. század elejéig a fizikában rend volt. Létezett kétféle kölcsönhatás, a gravitáció és az elektromagnetizmus, és azt hittük, hogy mind a kettőt jól ismerjük. Az elektrodinamikának Maxwell adta meg a ma is érvényes formáját, ami után még a kovariáns átírás következett. A régebbről ismert gravitációval, kevés probléma akadt. A newtoni erőtörvény megértette velünk az égitestek mozgását, csak a Merkúr perihélium precessziójánál vettünk észre némi problémát. Ez a rend a század első évtizedeiben hamar felborult. Elsőnek Max Planck fedezett fel egy állandót /1900/ a fekete testek sugárzásánál, a h-t. Két évre rá Lénard Fülöp megfigyelte a fényelektromos hatást. Ezután megváltozott az elektromágneses mező képe: a fénykvantum hipotézisből eredően /A. Einstein, 1905/ az e-mezőt kvantálni kellett, mert csak így tudtuk megérteni a fénnyel összefüggő jelenségeket. A Speciális Relativitáselmélet megfogalmazása után /H. A. Lorentz, J. H. Poincaré, A. Einstein, 1905/, 1916-ban a gravitációs mező képe is megváltozott. A tehetetlen és a súlyos (gravitációs) tömeg feltételezett ekvivalenciájára építve, Einstein kifejtette, hogy a gravitáció nem más, mint a fizikai tér tömegek körüli görbülése. A mai napig is elfogadott az a nézet a fizikában, hogy ilyen formában a két fundamentális mező a természeti jelenségeket jól leírja.

A 30-as évek elejétől, az atommagok összetevőitől kezdve az instabil részecskékig,  minden részecskét, mint mezőt kvantáltunk, [6]. A kölcsönhatást úgy képzeltük el, hogy a részecskék képződnek és annihilálódnak, az E = mc meghatározásában. A század 60-as éveinek közepéig megismertünk kb. 200 új részecskét. A stabil részecskék közül négyen tömeggel ellátottak, a tömegnélküliek, pedig a foton és a neutrínók. A többiek meg instabil részecskék és rezonanciák voltak, felruházva kvantumszámokkal és sok esetben jóval kevesebb, mint 2.2x10s élettartammal. Ez már sok volt. A tömeggel ellátott részecskéknél alapvető összetevőkre gondoltak a kutatók, hogy a részecskerend egyszerűbb legyen és megjelentek a kvarkok. Ezek először hárman voltak, majd mind többen lettek; és ma sem tudjuk hányan vannak. A kvarkok után következtek a próbálkozások a húrokkal, mint fundamentális részecskékkel. Ez a mai állapot a részecskefizikában, kb. 300 részecskével. Még nincs véglegesen eldöntve miből is áll az Univerzum, [1, 2], de egy alapvető problémát mindenki tisztán lát: a gravitációt nem tudtuk beépíteni ebbe a képbe, mert nem tudtuk a gravitációs mezőt kvantálni.

A kvark elméletet először az instabil részecskék tömege és élettartama közötti relációkon próbálták ki. A próbálkozások többé-kevésbé kielégítő eredményt szolgáltattak, és szalonképessé tették a kvarkokat. A kvarkok megszületése idejében, én az instabil részecskék tulajdonságait analizáltam. Feltűnt, hogy a relációknál használt alapvető fogalmak nincsenek tisztázva: az „élettartam” a kvantummechanikában és a „tömeg” fogalom még a klasszikus fizikában sem. Emellett hiányzott egy általános elv is, ami közvetlen meghatározta volna az instabil részecskék tömegét és élettartamát. A mikroszkopikus rezonanciák konzisztens leírásánál a probléma engem a Hamilton elvhez vezetett, amit egy véges térben fogalmaztam meg. Ez egy nyílt fizikai rendszer variációs problémája, [4, 5]. Sikerült a rezonanciák két paraméterét fixálni, az energiáját (= tömeg?) és az élettartamát. A variációs számítások megoldásai viszont tartalmazták az instabil állapotok mellett a kötött állapotokat is. Mivel a nyílt rendszerből kiinduló elmélet nem az energia kvantálásnak felel meg, felmerült bennem, hogy talán nincs is szükség a fizikában a foton hipotézisre. Az a megfigyelésem is, hogy minden mikroszkopikus rendszer nagyságrenddel kisebb, mint az általa kibocsátott fény hullámhossza, alátámasztotta ezt. Az eikonálelv szerint a kibocsátott fénynek hullám tulajdonsága van, és a részecsketulajdonságát ki lehet zárni. Közvetlen következményképpen a foton elképzelést a fizikában fel kell adni, [7]. Fel kell adni, mert a kibocsátott fény túl hosszúhullámúnak tűnik, ezért a kibocsátott fény csak hullámtulajdonságú lehet, és ezzel a részecsketulajdonság kizárt. Ha nincsenek fotonok, az ellenkező töltéssel és azonos tömeggel ellátott részecskepárok a találkozásuknál nem semmisülhetnek meg. Ilyen az elektron (e) és pozitron (p) meg a proton (P) és elton (E) (ez egy negatív töltésű proton). Az „annihilálódásnál” az elektromos elemi töltésnek is meg kellett volna szűnnie, amit nehéz elképzelni. A részecskepárok a találkozásuknál képeznek semleges és „tömegnélküli” részecskéket. Ismerünk is ilyen részecskéket, ezek a neutrínók. A neutrínók hiányzó tömege engem arra az elképzelésre ösztökélt, hogy a négy stabil részecskének, az elektromos töltés mellett, gravitációs töltésüknek is kell lennie, ellenkező előjellel és ezek a töltések is invariáns mennyiségek. Továbbá, az elektromos töltések mintájára elképzeltem, hogy a gravitációt ezek az elemi gravitációs töltések okozzák és nem a tér görbülése. Ez lényegbevágóan új a fizikában, ezért megvizsgáltam, hogy a tehetetlen tömeg és a gravitációs tömeg tényleg azonos-e, amit az Ekvivalencia Elv feltételez a természetben. A kutatásom eredménye az lett, hogy a kétfajta tömeg nem azonos. Ezt egy különböző anyagokkal ellátott ejtési kísérletem 2004-ben alá is támasztotta, [8]. Tehát a gravitációs töltések okozzák a gravitációs mezőt, hasonlóan, mint ahogy az elektromos töltések az elektromágneses mezőt hozzák létre. A négy stabil részecske kétfajta elemi töltése okozza a két alapvető mező szerkezetét.

Az előzetes dolgozatomban megadtam a két nem-konzervatív mező egyesített leírását, [9], amit egy kovariáns Lagrange függvény szögez le a Minkowski térben, egy véges tér-idő  tartományban. Az invariáns töltések a Hamilon elvnek mellék- és határ-feltételeket adnak, amik valós és komplex értékű Lagrange multiplikátorokat produkálnak, de ezek nem diszkrét energiaértékek. Az általános elmélet egy hipotézis megfogalmazására bátorított fel: a két alapvető mezőn és a négy stabil elemi részecskén kívül más fundamentális mező, és további elemi részecske nincs a természetben és a részecskéknek a kétfajta elemi töltésen kívül más tulajdonsága nincs. Ezt a hipotézist támasztom alá ebben a dolgozatomban azzal, hogy magyarázatot adok a fény, hullámszerű kibocsátására és a vonal spektrumok felbontására spin hipotézis nélkül. Továbbá a neutrínók közvetítésével magerőt, az ún. gyenge- és erőskölcsönhatást és az instabil részecskék szerkezetét magyarázom meg. Ennél a törekvésnél nagy szerepet játszik egy új fundamentális állandó h= q/2cx 1/ = h/387.7, ami a két alapvető neutrínó, = (e,p) és = (P,E), fellépését idézi elő. A h a határozatlansági reláció egy általánosabb megfogalmazásából ered, mint a heisenbergi határozatlansági reláció: egy elemi részecske helyét és a sebességét elvileg nem lehet pontosan meghatározni. Heisenberg tudvalevőleg a kvantummechanikában összekapcsolta a részecskék helyének és impulzusának bizonytalanságát a Planck állandóval.

Először a mezők egyesített leírásának az összefoglalását adom elő.

A kovariáns gravitációs mező és az egyesített mező elmélet

Kiindulva a gravitációs állandóból,

G  = g/4,                                                                               (1)

és a gravitációs töltésekből, g = gM, g = gm, a statikus gravitációs erő felírása

F = - g g /4r,                                                                  (2)

a newtoni erőnek felel meg, csak pozitív g-töltéseket feltételezve de én a tehetetlen és a gravitációs (súlyos) tömeget megkülönböztettem. A mínusz előjel arra utal, hogy az azonos előjelű g-töltések vonzzák, az ellenkező előjelűek, pedig taszítják egymást. A négy stabil részecske elemi gravitációs töltései okozzák a gravitációs mezőt. Az elemi gravitációs töltésekre a következőt tételezem fel

g = - g m,    g = + g m,      g = + g m,      g = - g m, (3)

|g| = m/ mx |g| = 1836.1527 x |g|.                                  (3’)

Az m az elektronnak (e) és a pozitronnak (p) az m pedig a protonnak (P) és az eltonnak (E) a tömegét jelenti. A fajlagos gravitációs töltést a g adja meg, éppúgy, mint a q/més q/m a fajlagos elektromos töltést. A fajlagos gravitációs töltés kifejezi a gravitációs állandót (1). A G egy természeti állandó, mert ez az elemi gravitációs töltésekből ered, amik invariánsak. A newtoni állandó G viszont nem volt egy természeti állandó.

Az nem-konzervatív elektromágneses mezőnek (e-mező) és a gravitációs mezőnek (g-mező) nagyon hasonló a szerkezete [7]. A két mező forrásait a kétfajta invariáns töltés képezi és a négy stabil elemi részecske (e, p, P és E) e kétfajta elemi töltés hordozója. Az elemi töltések mindegyike egy ún. Maxwell töltés, amit az jellemez, hogy egy jelenlévő külső mezőben egy és ugyanazzal a c terjedési sebességgel, izotrop mező hullámokat sugárzik ki, a töltések sebességétől függetlenül. A c egy további invariánsa az egyesített mezőknek Továbbá feltételezem, hogy a négy stabil részecskének e tulajdonságain kívül más tulajdonsága nincs.

A két mező csak abban különbözik, hogy az elemi töltések felosztása más, és a gravitációs mező egyenletében a gravitációs töltéssűrűségből és áramsűrűségből álló kovariáns négyes-vektornak, a j-nek negatív előjele van. Nem okoz semmi problémát a mezőegyenletek felírása a Maxwell-féle formában, vagy kovariánsan, a négyes-mezővektorok A, A segítségével. Itt csak a g-mező egyenletét (7) adom meg  a feltételekkel

a) j= (,j/c) ,          b) A= (,A/c),          (4)

a) j = 0,                        b) A = 0,                     (5)

dx = -j.ds ={ng},   a g = négy elemi g-töltés,           (6)

A = - j.                                                            (7)

A (7)-ben található mínusz előjel kivételével ezek teljesen megegyeznek az e-mező egyenleteivel, de alapvetően különböznek Einstein gravitációs egyenletétől, levezetve a feltételezett de a természetben nem létező Ekvivalencia Elvből.

Kiegészítésképp megadom az elemi gravitációs töltések definícióját is

dx = -E.ds = g,   
g= {-gm, +gm, +gm -gm},  i = 1, 4,                                 (8)

ami a (2)-ből adódik. Ebben az egyenletben feltűnik, hasonlóan, mint az elektromos elemi töltéseknél, hogy a mezők megfogalmazásánál nincs szükség az elemi töltés pontos helyének az ismeretére, elég az, hogy a töltés egy V térfogatban van. Ez a már említett hipotézissal konzisztens: a kétfajta töltést hordozó elemi részecskéknek sem a helye, sem a sebessége elvileg pontosan nem meghatározható. Ez tehát nem mond ellent a mezők egyenleteinek, és utat nyit a Planck állandó mellett egy további, ennél jóval kisebb állandó, a h, felé.

A mezők felírása tenzor formában

F = A- A,                                                 (9)

F = A- A,                                              (10)

egy kovariáns Lagrange függvényt definiál, egy véges tér-idő  tartományban:

L = -{ F F+ F F}/4
                    + { jA- jA}.                             (11)

Az L Euler-Lagrange egyenletei megfelelnek az e-mező és g-mező mezőegyenleteinek. Egy töltés nélküli -ban, ahol a j = 0 és a j = 0, két hullámegyenlet létezik ugyanazzal a c terjedési sebességgel. A fizikai vákuumot viszont meg kell különböztetni az elméleti vákuumtól, mert a fizikai vákuum tartalmazza például a neutrínókat is. A két fundamentális mező alapvetően nem-konzervatív, mert tartalmaz egy mágneses és egy gravitatív-mágneses komponenst. A mozgó részecskék ezek a komponensek segítségével kisugároznak elektromágneses és gravitációs hullámokat. A mezőegyenlet (7) megadja a gravitációs hullámok leírását is, ha j = 0.

Ha egy véges V térfogat csak egyfajta elemi részecskét tartalmaz, akkor a  és  töltéssűrűségek felírhatók a  részecskesűrűségekkel

 = q,      = g,
i = 1, 4, a négy fajta részecske,                                                     (12)

ahol q és g az i részecske elemi töltéseit jelenti. A négy   segítségével egy V térfogatban mindenféle kombináció felírható. Megfordítva, a j és  j áramsűrűség vektorok is felírhatók a négy j részecskeáramsűrűség vektorral,

j  = q j ,       j  = g j ,           i = 1, 4.                     (12’)

A részecskék két invariáns elemi töltése miatt, az integrált kontinuitási egyenletek

dx = -j.ds = {n},              i = 1, 4,         (13)

összekötött mellékfeltételeket és határfeltételeket adnak a Hamilton elvből

I = d(x) L(x)  =  d(x) {L (x)- L (x)}  = extremum,     (14)

kiinduló variációs számítás extrémum problémáihoz. Az L függvény az -ban tartózkodó részecskehalmaz kinetikus tulajdonságát írja le. A d(x)-t az invariáns infinitezimális térfogatot valamint a d(x) = (dx-(cdt)) az infinitezimális invariáns távolságot jelenti a Minkowski térben, ahol a mezők egyesített leírása van felállítva.

A fizikában állíthatjuk azt, hogy egy proton vagy -részecske elhagyja az atommagot, egy elektron az atomot és egy üstökös a Nap vonzáskörzetét annak ellenére, hogy a statikus erőket végtelen hatótávolságúaknak véljük. Az egyesített mező elmélet ennek a nézetnek is megfelel, mert teljesíti a szeparáció elvet, hogy a mezők véges propagációja és az -ban létező külső környezet hatása miatt, mindig lehet egy olyan véges -t találni, ami felületén az  –ban tartózkodó részecskehalmaz felbomlott részei között nincs már kölcsönhatás. A szeparáció elv a statikus Coulomb erőt és newtoni erőt nagy távolságokban megszünteti. Az összetett mellék- és határfeltételekhez (13) mindig lehet egy véges –ban felállítani, ahol a „kifutó” határfeltételek természetes határfeltételeknek felelnek meg egy V térfogat felületén. Azt a variációs elméletekből alapvetően tudjuk [3], hogy természetes határfeltételek a Hamilton elvnek  Lagrange multiplikátorokat adnak. A -k lehetnek valós vagy komplex értékűek [4]. Az elmondottak után nyilvánvaló, hogy a -k nem energia sajátértékek, a diszkrét  értékek fellépése nem felel meg energiakvantálásnak. Az egyesített mező eddig megtalált két alapvető állandója, a h és a h, az általános Hamilton elv Lagrange multiplikátoraiból származik, egy mikroszópikus véges négy dimenzionális tér-idő  tartományban.

A kötött állapotoknak megfelelő mellék- és határfeltételek

dx  = konst,   j.ds = 0,
i = 1, 4, a négy fajta részecske,                                                  (15)

a variációs számítás isoperimetrikus problémáját adják meg, ami lényegében már Euler-Lagrange idejében is megoldott volt [3]. Az általános feltétel (13), ami természetes határfeltételeket tartalmaz, még a matematikában is kevésbé ismert. E feltétel komplex értékű Lagrange multiplikátorjainak az imaginárius része adja meg az élettartamot [7]. Ezt az általános elméleti fogalmazást tartalmazza a disszertációm a mikroszkópikus fizikai rezonanciák problémája konzisztens leírásánál [4]. A numerikus megoldások nem okoznak különös problémát, mindegy, hogy a  komplex vagy valós az értékű [5], de a szigorú matematikai kezelése is még kifejlesztésre vár.

A Lagrange függvényben (11) a L kifejezhető a  és  j-kel és az elemi töltésekkel. A Hamilton elvre alapuló mező elmélet teljes kezelhetőségéhez csak az hiányzik, hogy a részecskesűrűségeket  és az áramsűrűség vektorokat j egy és ugyanazzal a függvénnyel ki tudjuk fejezni. Ez egy nem-triviális probléma, mert a  és a j alapvetően két különböző mennyiség, amelyeket általánosan külön-külön kell megadni. A probléma hasonló a klasszikus fizika pontszerű testek helyének és sebességének a szimultán megadásához. Csak abban az esetben adható meg a  és a  j egy közös (x) függvénnyel, ha ez a függvény a Hamilton elv egy stacionáris megoldása. Az általános esetben aztán a  és a j megadható a stacionáris függvények szuperpozíciójával egy véges -ban. Itt abból kell kiindulni, hogy a (x) lényegében csak az egyik alapvető állandót, a h-t vagy a h-t, tartalmazza. A formalizmus akkor lesz teljes az összes mikroszkópikus jelenség leírásához, ha az L megadása mellett még az az alapvető hipotézis is hozzáadódik, hogy más kölcsönhatás, mint a két fundamentális kölcsönhatás, és más részecske, mint a négy elemi részecske e, p, P és E, a természetben nem létezik és ezeknek csak kétfajta elemi töltésük van.

 

 

 

Határfeltételek és a sajátérték probléma stacionáris megoldásai

Az egyesített mezőknél a Hamilton elvből kiinduló variációs problémához, az invariáns töltések miatt, összekötött mellék- és határfeltételek (13) tartoznak. A variációs probléma a Minkowski tér egy véges  tartományában van felállítva. A variációs probléma megoldásait a szeparáció elv garantálja. Az  felülete a Minkowski teret két részre osztja fel, egy belső és egy  külső részre. Egy fizikai probléma konkrét kezelése a tér és idő kontinuum felosztásában, egy véges -ra és egy külső tartományra , egy lényeges felismerés. A külső részben a végtelen Univerzum van, végtelen sok részecskével. A belő részben meg mindig csak egy véges számú elemi részecske állhat. Az Univerzum hatását az  térfogatban és ennek a felületén, a „külső környezet hatásának” nevezem és ezt feltételezésekkel kell kezelni. A fizika csak az -ban tartózkodó részecske­halmazokkal foglalkozik. A tér és idő kontinuum felosztásánál mindig használni kell egy megadott időskálának és koordinátarendszernek a kezdőpontját, ami egy az -val rögzített, kitüntetett vonatkoztatási rendszer használatát írja elő. Ennek hátterében kell azokat a részecskefizikában gyakran idézett állításokat látni, hogy a megmaradási törvények szimmetriákból levezethetők, amit én lényegében visszautasítok. Ezen állítások szerint például az energia- és impulzusmegmaradás levezethető abból a szimmetriából, hogy a fizikai törvények nem függenek attól, hol vesszük fel t = 0-át és r = 0-át. Az az álláspont sem mérvadó, hogy a Maxwell-egyenletek mértékszimmetriája – amely az elektrosztatikus tér esetében a potenciál zéruspontjának szabad választását jelenti – az elektromos töltés megmaradásához vezet. A töltések megmaradása az elemi töltések invariáns axiómájából eredeztetik. Ez a megmaradási törvény a mező tulajdonsága, és nem egy szimmetria elv következménye. A szimmetriákból semmit sem tudunk meg az anyag alapvető tulajdonságairól, a kölcsönhatásokról és a tömegekről. Az energia- és impulzusmegmaradás azért sem használható, mert a részecskék közötti kölcsönhatást közvetítő egyesített mező alapvetően nem-konzervatív. A részecskefizikában nem használhatóak a szimmetriákból eredeztetett megmaradási törvények.

Most a külső környezet hatását analizálom az -ban. Egy feltevés, amiből kiindulhatunk az lehet, hogy az -ból teljesen kizárjuk a külső környezet hatását. Ebben az esetben a véges térfogat felületén, a szeparáció elv alapján, a külső környezet hatása és a belső erők egymást kiegyenlítik. Mivel a variációs problémát egy véges -ban kezeljük, a határfeltételekre gondolva, ebben az esetben azt állíthatjuk, hogy a határfeltételek nem függenek az  felületétől, és ezen a felületen a szétbomlott részecskehalmazok közötti kölcsönhatásoktól. Ennek megfelelően a végtelen hatótávolságúnak vélt statikus Coulomb és newtoni erőket teljesen leárnyékoltnak tekinthetem az  felületén. Ennek a legegyszerűbb feltevésnek az a továbbmenő általánosítása, ha a külső hatást, mint egy állandó mezőt kezeljük az -ban. Csak a mágneses mezővel ez a feltevés a Zeeman effektus, és csak az elektromos mezővel a Stark effektus magyarázatához vezet, a vonal spektrumok megfigyelt tulajdonságainál.

Egy másik feltevésnél abból indulunk ki, hogy a véges  térfogatban „bezárt” rendszer egyensúlyban áll a külső környezettel. Az egyensúlyi állapotnál további felosztást kell tenni. Egy egyensúlyi feltevés lehet az, hogy az -ban a „bezárt” részecskehalmaz a külső mezőkkel egyensúlyban áll és nincsenek részecskék kicserélve. Ha az -ban csak az elektromágneses mező hatását akarjuk elemezni, akkor egy olyan problémát izoláltunk, ami megfelel a fekete testek sugárzásának. Max Planck sugárzási törvénye, ami a h állandó felfedezéséhez vezetett, ennek a feltevésnek felel meg. Egy másik egyensúlyi állapotnál abból a feltevésből indulunk ki, hogy az -ban „bezárt” rendszer és a külső környezet elektromosan semleges részecskéket is, pl. neutrínókat, kicserélhet. Ez a feltevés a természetben előforduló stabil atommagok problémájához vezet, és itt a mezők egyensúlya is feltételezett, akkor is, ha ez explicit nincs kezelve.

Az is feltételezhető, hogy az  felületén csak egyfajta elemi részecske hatol be, pl. csak elektronok. Az -t ekkor csak azok a részecskék hagyhatják el, amik az -ban bent voltak, plusz a behatoló részecske. Ezzel a részecskeszórás problémáját izoláltuk és ennek egy különös esete az, ha csak a behatoló részecskét akarjuk, mint kimenő részecskét kezelni. Ez például az elektron- vagy a protonszórás esete.

A külső környezet hatása kezelésétől függően tehát más-más fizikai problémát izolálhatunk a Lagrange függvény L használatánál. Ha a behatoló részecskéket kizártuk, akkor a részecskeszámok vagy állandók maradnak az -ban, vagy egy olyan állapotot izoláltunk, ahol mint kimenő részecskék csak az -ban tartózkodó részecskék léphetnek fel. Az első eset a részecskehalmaz kötött állapotát fogalmazza meg. A második eset, pedig megfelel a részecskehalmaz „instabil állapotának”, ami a radioaktív magoknál és az „instabil részecskéknél” mutatkozik meg. A probléma megoldása függ a mellék- és határfeltételektől. Az „instabil állapotnál” az integrált kontinuitási egyenletek (13) kimondják, hogy az  felületén kimenő részecskék csökkentik a belül levő részecskék számát. Ezt a csökkenést az „instabil állapot”  élettartama adja meg. A -nak csak abban az esetben van leszögező értelme, ha kezdetben az -ban, csak egy bizonyos típusú és bizonyos számú elemi részecskét tételeztünk fel. Ebben az esetben a variációs probléma stacionárius megoldása egy komplex -t ad, aminek két valós része az instabil stacionárius állapot „energiájának” E és élettartamának  felel meg. Ezek az itt lerögzített fogalmak használata szükséges a formalizmus továbbfejlesztésénél a magfizika és részecskefizika „instabil állapotaihoz”.

A mezőegyenleteknél, amik a Hamilton elv (14) Euler-Lagrange egyenletei, csak az L játszik egy szerepet. Ha viszont a Hamilton elvből a részecskék mozgásegyenleteit akarjuk levezetni, akkor a Lagrange függvény kinetikai részének az ismerete is szükséges. Mivel elvárható, hogy az L-ben a tehetetlen tömegek szerepelnek, és ezeket csak az elemi részecskéknél ismerjük – csak az elemi részecskéknél azonos a nyugalmi tehetetlen tömeg a gravitációs tömeggel –  az általános esetben közelítéseket kell alkalmazni az L-re.

A továbbiakban csak a két-részecske problémával fogok foglalkozni, ahol az L ismerete nem problematikus. Mivel a kölcsönhatások csak a két részecske közötti relatívvektortól függenek bevezetem az x relatívvektort. Az i részecske relatív állapotát a másik részecskével szemben az -ban, a egy kompex értékű (x) függvénnyel fejezem ki, ami a részecskesűrűséget következőképpen

(x) = *(x)(x),                                                        (16)

adja meg. A következő lépésnél egy matematikai hipotézist használok fel, ami kimondja azt, hogy a (14) Hamilton elvből eredő variációs problémánk stacionáris megoldásai mindig felírhatók a következő szeparálással az -ban, és kizárólag csak ott

(x) = (,x)xexp(-it).                                              (17)

A  a Lagrange multiplikátornak felel meg az adott fizikai rendszernél a véges tér-idő tartományban. Ez a feltevés a mi Lagrange függvényünkre (11)

L( x) = L (x)- L (x),

tudtommal a matematikában sincs általánosan bebizonyítva. A (17)-ben feltételezett x és t változók szeparálásának az a következménye a stacionáris megoldásoknál, hogy a -k segítségével a variációs probléma megoldását átvihetjük a három dimenziós x-térbe, és a természetes határfeltételt egy véges V térfogat felületén értelmezhetjük. A kvantummechanikában a stacionáris állapotok exponenciális idő függvénye, a

 = h/2,           h a Planck állandó,                               (18)

Lagrange multiplikátort használja, de ez itt nem az energia kvantálását jelenti.

Itt meg állunk egy pillanatra, mert meg lehet említeni azokat az egyszerűsítéseket, amik az általános Hamilton elvből (14) kiindulva a hidrogénatom Schrödinger egyenletéhez vezetnek. A Schrödinger variációs megfogalmazásának az összevetését az új Hamilton elvvel a [7] idézet első cikke ismerteti részletesebben. Ott az első helyen a gravitáció teljes elhanyagolása megemlítendő. Mivel a Schrödinger egyenlet csak az elektron állapotát vette tervbe leírni, az e-mező tenzor formájú felírásának a mellőzése a Lagrange függvényben megemlítendő. A még hátra maradt kovariáns Hamilton elv

I =d(x) {L (x) - jA} = extremum,

a kötött állapotoknak megfelelő mellék- és határfeltételek mellett az elektron és a proton stacionáris állapotára

j.ds = 0 dx  = konst,  i = 1,  és i = 3,

akkor, ha a részecske sűrűségek (x) = *(x)(x) felírhatók mint (x) =  (,x) x exp(-it) valós értékű -val. Most már áttérhetünk lassan a nem-relatívisztikus közelítéshez. Egy tömegközépponti koordinátarendszerben csak az elektron relatív koordinátájávál r, a redukált tömeggel m’ és az elektron függvényével (r,t) = (,r) x exp(-it) számolunk tovább. A (,r) függvény Wronski determinánsára még szükség lesz, mert ez automatikusan teljesíti az elektromos töltés folytonossági egyenletét. A Wronski determináns segítségével fogjuk az áramsűrűséget j a (,r)-val kifejezni

j = q j = i q / 2 m’ (Ñ*. - * .Ñ ),

és a folytonossági egyenlet j = 0 egy mellékfeltételt jelent a (r,t)-nek. A megcélozott koordinátarendszerben és kifejezve a (,r) függvénnyel a redukált tömeggel m’,  a folytonossági egyenlet j = q /c { j /t +div} = 0  és (17) után

 j /t = /2 m’ (Ñ(,r) *.(,r) - (,r)* .Ñ (,r)) = - div,

következik.

A kovariáns  jA = q (+j A) kifejezésnél a j A szorzatnak megfelelő tag a mágneses mező jelenlétét is figyelemben veszi. A Schrödinger levezetés egyszerűen ignorálta a mágneses mező jelenlétét. Mivel ott ez a tag nem lép fel, később ad hoc be kellet vezetni az elektron önperdületét (spinjét), hogy a kísérletekben észlelt spektrumokat értelmezni tudjuk. Hiányzik még az L(x) nem-relatívisztikus közelítése, amire a következő kifejezést írt fel Schrödinger

L= const (Ñ* Ñ ).

Végül meg kell említeni, hogy a Schrödinger variációs megfogalmazása a végtelen |r| térfogatra lett felírva, amíg itt egy véges -ra értendő a variációs számítás.

A -knak van egy másik felosztása is, egy  állandóra, ami csak az -ban lévő  részecskerendszertől, és egy -re, ami meg a rendszer térbeli eloszlásától függ

 =  .                                                                            (18’)

Ez a felosztás akkor célszerű, ha egy adott rendszer ismert a Lagrange multiplikátort megadó kifejezéséből egy másik rendszerre akarunk általánosítani. A (18’) felosztást fogom használni, amikor a H-atom Lagrange multiplikátorában fellépő Planck állandóból a h-ra fogok következtetni. A h Planck állandót és a h-t a Lagrange multiplikátor  két különböző értékének tekintem, az első esetben az atomokra a második esetben meg a neutínókra ill. a stabil neutronra értve. A Planck állandóban a H-atomnál

h = q/2c x (m’c/2E),                                              (19)

a q és c invariáns mennyiségen kívül még a H-atom redukált tömege, m’, és az ionizációs energiája, E, szerepel. A kifejezés

m’ c /2E,                                                                       (20)

ugyan egy állandó, de nem egy invariáns mennyiség. Az E össze van kötve egy kitüntetett koordináta rendszerrel meg a részecskerendszer tömegközéppontjával. Más rendszernél más a redukált tömeg és az alapállapot ionizációs energiája. Látni fogjuk, hogy a h-ból a tömeg ki fog esni és így a h csak két invariánstól, q és c, függ. Itt kihasználjuk azt a megfigyelést, hogy az elemi g-töltések legalább egy elképzelhetetlen nagy faktorral 10 kisebbek, mint az elemi e-töltések |g(j)| << |q(j)|.

A stacionáris megoldásoknak kétféle formája van. Az egyiknél az  értéke egy valós szám, a másiknál meg egy komplex értéket vesz fel. A valós értékek megfelelnek az ún. kötött állapotoknak, a komplex értékek meg az „instabil állapotokat” rögzítik. Mivel a kötött állapotokat az egyesített mező elméletnek a kvantummechnikára gyakorolt kihatásánál fogom részletesen tárgyalni, most ezt itt nem is követem tovább.

Az „instabil állapotoknál” fellépő komplex -nál (18’) a reális rész, Re(), és az imaginárius rész, Im(), csak olyan értéket vehet fel, ami a kontinuitási egyenlettel megegyezik. Nyilvánvaló, hogy az  i részecske idő változása a V térfogatban

dx(; x,t)  =
-dx (; x,t),  t >t,                                    (21)

az exponenciális bomló függvénynek

N(t) = N exp{-(t- t)/},                 t >t ,                            (22)

felel meg. A   bomlásidő, vagy élettartam, értéke (17) és (18’) után

(; x,t) -(; x,t) =
|(,x)|exp{-2Im()(t- t)},                                     (23)

ami (21) értelmében  = 1/{2Im()}>0. A stacionáris megoldást az x térben célszerűbb a  =  helyett egy másik komplex értékkel, a K-val, megadni, amivel

 (K; x) = *(K,x) (K,x).                                 (24)

A stacionáris függvény (k,x) természetes határfeltétele a V felületén átmegy a

n. (K ,x)- i n .K (K,x) = 0,                                     (25)

feltételbe, ahol n egy radiálisan kifelé mutató egységvektor. Ez a komplex értékű függvénynek (K,x) az általánosított természetes határfeltétele. A stacionáris megoldásoknál, amik a rendszer „instabil állapotainak” felelnek meg,

K = k –i ,         k>0,               >0,                          (26)

és

 =  = K = k- -i(2 k),
 = 1/4k>0.                                                                    (27)

Az integrált kontinuitási egyenlet (13) után

( K; x,t) -( K; x,t) =
- dt j (K; x,t).ds.                                                  (28)

az i részecskét „kivándorlását” adja meg a V térfogatból a t > t időben.

Összefoglalás: Egy Lorentz kovariáns Hamilton elvet fogalmaztam meg az egyesített, nem-konzervatív e- és g-mezőre a Minkowski-tér egy véges  tartományában. A Hamilton elv, az invariáns töltések miatt, stracionáris függvényeket definiál. Az elméletben csak invariáns mennyiségek (q, g, i = 1, 4 és c) és valós vagy komplex értékű Lagrange multiplikátorok lépnek fel. Az általánosított határozatlansági reláció és a szeparáció elv az egyesített mezőkkel összhangban van. Ezzel a formalizmussal felfegyverkezve látok hozzá a mikrokozmosz konzisztens leírásához.

 

Az egyesített mező elmélet kihatása a kvantumfizikára

A kvantumfizikára gyakorolt első lényeges kihatást a határozatlansági reláció adja meg:  Az elemi részecskéknek sem a helyét, sem a sebességét nem lehet elvileg pontosan meghatározni. Ez egy általánosabb megfogalmazás, mint Heisenberg határozatlansági relációja /W. K. Heisenberg, 1901-1975/, a h Planck állandóval /M. Planck, 1858-1947/. Annak ellenére, hogy a h csak az atomok, és molekulák világában uralkodik és a kvantummechanika csak a Planck állandó kihatásával foglalkozik a mikroszkópikus fizikában, mégis a h jelentősége általánosítva lett az atommagokra is. (Heisenberg megállapítása az volt 1932-ben, hogy az elektron nem fordulhat elő a magban.) Ezt az általánosítást nem tartom helytállónak, mert ott egy 387.7-szer kisebb állandó, a h, dominál. Ebből is látható, hogy a mikroszkópikus jelenségeknél az alapálláspontok lényegesen megváltoztak az egyesített mező elméletben. 

A mikroszkópikus rendszerek nyílt rendszereknek felelnek meg, egy véges tér-idő  tartományban. Azt alapvetően tudjuk, hogy nyílt fizikai rendszerek nem-konzervatívak, és az energia nem egy állandó mennyiség. Ráadásul, a fundamentális mezőknek a nem-konzervatív komponense (a mágneses és a gravitatív-mágneses része) minden mozgó testnél sugárzást okoz, ami energiavesztéssel jár. Ha keresnénk az ilyen rendszerek energiáját klasszikusan mint állandót, vagy a mikroszkópikus rendszereknél kvantálva, az mindig csak közelítésnek felelne meg. A mikrokozmoszban az energiakvantum hipotézis nem fenntartható: A E = h energiával ellátott fotonok a természetben nem léteznek. Mikroszkopikus rendszereknél, csak az alapállapot energiája megközelítőleg állandó. Ilyen feltételek mellett a Lagrange formalizmust /J. L. Lagrange, 1736-1813/ kell felhasználni a rendszer leírására, a Hamilton elvvel (14) egyetemben, /W. R. Hamilton, 1805-1865/. Az invariánsokkal ellátott Lagrange formalizmus általánosítható e nyílt és nem-konzervatív rendszerek leírására is. A szükséges mellék- és határfeltételek a kontinuitási egyenletekből (13) és a mezők Lorentz feltéleiből adódnak. A Planck állandó a természetes határfeltételekhez tartozó valós értékű Lagrange multiplikátorokon keresztül kerül be a formalizmusba, mint = h/2. A Lagrange multiplikátorok szerepe úgy is látható, hogy azok a természetes határfeltételek áttranszformálását adják meg állandókká. A foton hipotézist /Einstein, 1905/ fel kell adni a mikroszkopikus fizikában, mert az elektromágneses mező alapvetően egy nem-konzervatív és nem-kvantált mező. Mivel az e-mező nincs kvantálva, a természeti jelenségek magyarázatánál van még elég tennivalónk. Új magyarázatokat kell adni a fényemisszióra, a fekete testek sugárzására, a fényelektromos hatásra, a Franck-Hertz-, Stern-Gerlach-, Einstein-de-Haas-kísérletre, stb. a foton hipotézis nélkül. A Compton-effektus magyarázatát már Schrödinger, és később a fényelektromos effektus magyarázatát pl. Gong BingXin megadta [11] a klasszikus elektrodinamikán belül, akkor is ha Gong levezetéses ellentétben áll az elfogadott kvantummechnikai alapokkal.

Itt én csak a hidrogén atom foton nélküli fénykibocsátását fogom megtárgyalni, ami alapján a lényeg megérthető. Előre bocsátom, hogy a kb. 1 Å (1 Å = 10 cm) nagyságú H-atom által kibocsátott hullámhossz l mindig legalább három nagyságrenddel nagyobb, mint a H-atom. A legkisebb l =  927 Å annak a sugárzás hullámhosszának felel meg, ami a H-atom ionizálásához szükséges. Hasonló a helyzet minden más mikroszkópikus rendszernél is. Az eikonálelv miatt, nem csak az atomok fénykibocsátásánál, kell a fény hullámtulajdonságával 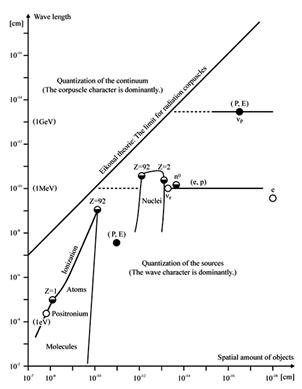számolni, hanem általában minden mikroszkópikus rendszernél.  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ábra 1. Összehasonlítás: hullámhossz + objektumok nagysága

A Lagrange multiplikátorok veszik át a sugárzás elméletben a döntő szerepet. Ennél a rendszer alapállapotának kitüntetett szerepe van. Ha a H-atomot egy stacionáris függvénnyel, a -gyel, írjuk le, gondolni kell arra, hogy a  az (e+P)-ből álló rendszer alapállapotának igazában ez csak egy megközelítése akkor, ha csak a Planck állandót vesszük figyelembe. Ilyen  értelemben a  a Hamilton elvnek (14) a  Lagrange mutiplikátor  = h/2 = -hoz tartozó stacionáris függvénye egy véges térfogatban. Tételezzük fel, hogy t< t időben a H-atomot nem érte külső hatás, nem volt gerjesztve. Akkor a H-atom a  alapállapotban van (az  függvények x változóját nem fogom itt jelölni) és az elektromos töltéssűrűség

(t) = q (t) = q(t) (t) =  q|| ,       t < t, (29)

sehol sem változik a V térfogatban, mert a stacionáris -nek az idő függvénye exp(-it) és itt csak az alapállapot (t) = exp(-it) szerepel. Mivel a töltéssűrűség (t), t < t, az időtől nem függ, a H-atom az alapállapotban nem is sugároz ki elektromágneses hullámokat, az energiája sem változik. (Az, hogy honnan kapjuk a -gyel összefüggő E  ionizációs energiát,  már más lapra tartozik.)

A gerjesztés után (t > t) a H-atom az alapállapotát elhagyja és a gerjesztett állapotba (t) megy át, amit a V térfogatban ki tudunk fejezni a többi  =  Lagrange mutiplikátorokhoz tartozó stacionáris  függvényekkel, mint szuperpozíció

(t) = a exp(-i (t-t)). +aexp(-i(t-t)). (30)

A gerjesztett állapotnak megfelelő (t)-t behelyettesítve (29)-be kapjuk, hogy a töltéssűrűség (t) a  = |-| rezgésszámokkal oszcillál. Az oszcilláló töltéssűrűség elektromágneses hullámokat bocsát ki, ezekkel a rezgésszámokkal, amiket a spektrométerek messze a H-atomtól regisztrálnak. A teljes vonal spektrum egyszerre jelenik meg spektrométerben, és csak a térfogat integráloktól

dx{a a},                                                           (31)

függ, hogy milyen nagyok az egyes vonalak intenzitásai.

 

 

 

 

 

 

 

 

 

 

 

 

 

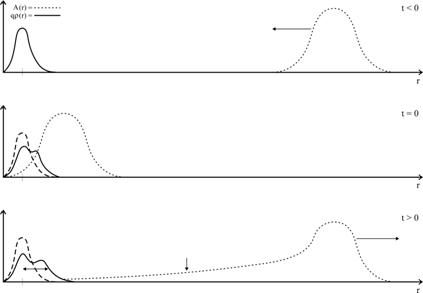
Ábra 2. A gerjesztés A(r) időbeli ábrázolása. A gerjesztés után
t>0 a töltéssűrűség q(r) oscillál és exponenciális fénykibocsátást okoz egy véges tér-idő tartományban.

A stacionáris állapotokat a V térfogatban természetesen felírhatjuk gömb- és radiális-függvényekkel. Ha n a radiálisfüggvények csomópotjati számolja a V-ben, akkor a kísérleteknél megállapíthatjuk, hogy a spektrométerek nagyobb, mint kb. n = 15 átmenethez tartozó rezgésszámokat soha nem mutattak ki a H-atomnál. Csak a kvantummechnika tankönyvek számolnak be a H-atomnak végtelen sok rezgésszámáról. A kísérletekben azt is megfigyeltük, hogy ha a hidrogéngáz nyomása növekedik a kísérletben, a magasabb átmenetek nem jelennek meg, és a vonalspektrum kiszélesedik. A nagyobb nyomásnál közelebb vannak az atomok egymáshoz, és így kisebb V térfogat áll rendelkezésre a stacionáris függvények meghatározásához. Tehát nem a radiálisfüggvények nullához tartása a végtelenben a mérvadó a fizikában, amit a Schrödinger egyenlet sajátérték megoldása tételez fel, hanem a természetes határ-feltételek egy véges V térfogat felületén. A kísérletekben észlelt fénykibocsátások mind a kovariáns Hamilton elv (14) döntő szerepét támasztják alá. A fénykibocsátás egy folytonos elektromágneses hullámokat okozó rezonanciajeleség egy véges térfogatból, és nem a fény kvantumféle emissziója.

Az atomok vonal spektrumját meghatározó Lagrange multiplikátorokon keresztül bekerülő Planck állandó nem lehet egyben az elemi részecskék tulajdonsága is. G. E. Uhlenbeck és S. A. Goudsmit feltételezése 1925-ből az elektron spinjével kapcsolatban, ami proporcionális a h-val egy nem helytálló feltevés. A vonal spektrum felhasadását a Lagrange fügvényben mindig jelenlévő mágneses mező Aokozza, a

j.A,                                                                                   (32)

term szerepében. Ez a term a -k számát és értékeit megváltoztatja. A mágneses mezőt a Schrödinger egyenlete is /E. Schrödinger, 1887-1961/ elfelejtette, mivel az csak az energia kvantálását célozta meg (1927) a Coulomb erővel.

Az előző fejezetben már kifejtettük, hogy a Hamilton elv stacionáris állapotainál az elektron áramsűrűség vektora j is kifejezhető a Lagrange multiplikátorokhoz tartozó stacionáris  függvényekkel. Az elektron elektromos áramsűrűsége, j, a gerjesztett állapotban és egy véges térfogatban definiálható a Planck állandóval mint szuperpozició

j = -q Re {*} =
-q Re {a**(a)}.                            (33)

Az H-atom alapállapotában a mozgó elektron (és a mozgó proton is) egy mágneses mezőt okoz, ami egy

m = -,                                                                        (34)

nagyságú mágneses momentumot ad meg. A gerjesztett állapotban (30) a mágneses momentumok szuperpozíciója szerepel. Az anormális Zeeman effektus az e-mező tulajdonságából ered a Hamilton elven keresztül. A négy elemi részecskének nincs saját impulzusmomentuma.

A Schrödinger egyenletből általánosított Hamilton operátor akalmazása a Hilbert-térben /D. Hilbert (1862-1943)/ csak mint egy közelítés értendő a kötött állapotokra. Ez a formalizmus csak zárt és konzervatív rendszerekre használható. Az is köztudomású, hogy Schrödiger egyenlete már a két elektronból álló hélium atomhéját sem tudja leírni. Az elmondottak alapján nem arról van szó, hogy egy kis baj van a kvantált elektromágneses mezővel, amelynek végtelen értékű integráljait a QED-ban csak renormalizálásokkal tudjuk kezelni, hanem arról, hogy a természetnek egyáltalán nincs szüksége kvantált mezőkre. Nincs szükség a Dirac /P. A. M. Dirac, 1931-1984/ egyenletre sem, hogy a relativisztikus elektront le tudjuk írni. A szabad elemi részecskék mozgását az egyenlet

j = + j = 0,                          (i  = 1 az elektron),

kitűnően leírja relatívisztikusan, de két független függvénnyel a -vel és a j-vel.

A H-atom fénykibocsátása tárgyalásánál az egyszerűsítéseket elhallgattam. Ezért most ezeket is röviden megemlítem. A Hamilton elvből eredő  stacionáris függvény, az elektront és protont összekötő relatívvektor segítségével lett megadva. Ez a relatívvektor átmegy a tömegközépponton, ami a térben nincs rögzítve, követi a H-atom mozgását. Ezenkívül az elektron térbeli mozgását a proton is követi. A gerjesztett állapotban a proton mozgása is okoz fénykisugárzást, amit észlelnek is a műszerek, gondoljunk csak a hiperfinom felhasadásra és a semleges hidrogén atom 21cm-es vonalára. Továbbá, a H-atomok tömegközéppontjai, a hidrogéngáz hőmérséklete miatt. különböző sebességgel mozognak. Ez a vonal a spektrum kiszélesedését és hősugárzást okoz.

Amikor a Schrödinger egyenletből a hidrogén atom spektrumának a magyarázata megszületett, akkor csak a Planck állandó h volt ismeretes, és a neutron felfedezése (J. Chadwick, 1932) is még távolabb volt. Én a hidrogén atomot úgy kezelem, hogy nála csak a Planck állandó játssza a stabilizáló szerepet. A következő fejezetben ismertetem az elektron és a proton egy másik kötött állapotát, a stabil neutront, amit a h okoz.

A neutrínók és a magerők az egyesített mező elméletben

A kvantummechanika revíziója után az atommagokra kihegyezett ismereteim összeállítás jön, ahol a h  és az elektronneutrínó =(e,p) veszi át a fő szerepet [7, 9]. Ez a nézet a szakközönségnél is kevésbé ismert. A neutrínók megfigyelésének kísérleti problémái a részecskék semleges és „tömegnélküli” tulajdonságából eredenek. A felírt magreakciókban gyakran nem is szerepelnek, pedig jelen vannak. Megemlítem, hogy a neutrínó hipotézis W. Paulitól (1900-1958) származik (1930) a magok -bomlása magyarázatánál. Pauli a neutrínót akkor a magból kijövő részecskének képzelte el. Egyidejűleg, a határozatlansági reláció használatában a Planck állandóval, Heisenberg feltételezése miatt, a magfizika kizárta az elektront az atommagból és az instabil neutront is, mint önálló elemi részecskét kezel a kísérleti felfedezése óta. Röviddel ezt követően, E. Fermi (1901-1954) a magok -bomlási elméletéből (1932) származtatva tekintették a fizikusok a neutrínót úgy, hogy ez a magban széteső neutronból képződik, egy protonnal és egy elektronnal együtt

 N  P  + e +,                                                                  
{szerintem a magban N = ( P,e,p,e) van jelen}.                  (35)

A neutrínó első közvetlen létezését csak 1955-ben tudta F. Reines és G. A. Cowan kísérletileg kimutatni a

P +  = N  +  p,                                                                           
{ahol szerintem a stabil neutron, N = ( P,e), szerepel},               (36)

reakcióban. Ezután a neutrínót már többször, pl. 1959-ben Csikai Gy. és Szalay S. is a

He  Li  + e + 
{ahol szerintem a neutrínó  = ( e,p) szerepel},                       (35’)

reakcióban, megfigyelték. Yukawa /H. Yukawa, 1907-1981/ a magerőt virtuálisan kibocsátott kb. 124 MeVc tömegű részecskék közvetítésével képzelte el 1934-ben. Az egyesített mező elméletben én feltételezem azt, hogy a  = (e,p) és az elektron az atommagban jelen vannak, ott a magerőt képezik és onnan jönnek ki a mag bomlásánál.

Kétfajta alapvető neutrínót ismertem fel, amik a két elemi részecskepárok

 = (e,p),                  és               = (P,E),                           (37)

stabil kötött alapállapotának felelnek meg a h közvetítésében. A részecskefizika ezt a neutrínó megkülönböztetést nem ismeri. A neutrínók elektromosan semlegesek és “tömeg-nélküliek” mert a nulla gravitációs töltésük miatt, a külső statikus gravitációs erőtér nem hat rájuk. A kettő neutrínó közül csak az elektronneutrínó  játszik szerepet a magokban. Mivel a h-n keresztül a  fellépését a magokban feltételezem, Heisenberg, Fermi és Yukawa feltevéseit el kell utasítanom. Én megkülönböztetem a stabil neutront N = (P,e) a magokban előforduló instabil neutrontól, ami négy elemi részecskéből áll

N = (P, 2e, p) = (P,, e).                                                (38)

Az elektronneutínóval én egy összekötő szerepet ismertem fel az instabil neutronban és az atommagban. Egy egyszerű fizikai ábrázolást fogok használni, hogy a -nek ezt a szerepét ábrázolni tudjam. A  mint az elektron és pozitron kötött állapota szerepel, ahol ezek a részecskék egy pályán - pl. egy körpályán r= 0.703x10 cm átmérővel - egymás után repülnek. A zárt pályán ezek a részecskék nem tudnak elektromágneses hullámot kisugározni, nem tudnak energiát veszteni. (Vagy ha kicsit eltér a pályájuk a zárt pályától, akkor csak kis mennyiségben tudnak sugározni.) Az atommagokban e pálya síkja ellenkező oldalán egy-egy jóval nehezebb proton (P,,P) helyezkedik el. Beépülhet a megnövekedett -pályába még egy elektron is és így a magban egy stabil P-P kötés (P,,e,P) = (N,P) képződik, kb. r = 1 fm P-pályasík távolságnál. A P-P kötéseket vagy egy  egyedül, de valószínűbben a (,e) képződmény adja. Nem csoda, hogy az atommagot egy instabil neutron is el tudja hagyni. Közben megismertük a deuteron szerkezetét is, ami összesen öt elemi részecskéből áll

D = (P,,e,P) = (N,P).                                                    (39)

A magsugár formula R = r A a stabil magoknál és az A tömegszámnál így megérthetővé vált. Lehet a  pálya egyik oldalán a proton helyett egy elton is, ami egy összetett neutrínót  = (P,,E) állít elő, de ez a képződmény már a részecskefizikához tartozik. Természetesen az (E,,E) és (E,,p,E) is felléphet, de ezek a kötések az ún. „anti-anyagban” szerepelnek. Az -nek az összekötő szerepét az atommagokban, mint „magerőt” észleljük, így szó sincs az egyesített mező elméletben virtuális részecskék kibocsátásáról a magerő magyarázatánál. Az elektronneutrínó átmérője r= 7.03x10 cm határozza meg az atommagok nagyságát, amit valamivel kisebbre számítottam ki, mint a legkisebb atommag nagysága.

A természet csak az (P,,e) és az (E,,p) összetételű anyagok stabil egymáshoz való kondenzálását engedi meg. Az Univerzumban kétféle “látható világ“ van, amelyek a gravitáció töltések ellenkező előjele miatt taszítják egymást, és amelyek jelenlétét a kibocsátott fény vöröseltolódása árulja el. Az Univerzumban az asztrofizikusok által sejtett “sötét anyag“ az (e,p)-ból és a (P,E)-ból áll, hozzávéve még a négy részecske  = (P,,E) kötött állapotát és az ezekhez hasonló összetételű, elektromosan semleges és tömegnélküli képződményeket. A „sötét anyag”-ban fellépő képződmények nem tudnak egymáshoz kondenzálódni, mert hiányzik közöttük a hosszú távolságokra ható statikus gravitációs erő, de valószínűleg összegyülekeznek a galaxisok anyaga körül.

Az elektromosan semleges izotópoknak a gravitációs tömege, amik ugyanannyi protonból és elektronból, és egy még ismeretlen M(A,Z) számú -ből állnak, az elemi gravitációs töltésekből kiszámítható. Az izotópok gravitációs töltése, a neutrínó nulla gravitációs töltése miatt, nem függ a magokban létező -k számától. Az A tömegszámnál és Z magtöltésnél a protonok az elektronok által leárnyékolt gravitációs töltés  

g = A (g +M (A,Z)(g + g)+ g) =  A g (m - m).     (40)

Ebből következtetve az izotópok gravitáció tömege m(A) = g/g csak a tömegszámtól

m(A) = A (m- m),                                                             (41)

függ. E szerint a hidrogén atom gravitációs tömege m(H) = (m-m). Az izotópoknál megmért tömeghiányra a következő képlet adódik ki

m (A,Z) = A m(H) (1 - (A,Z)).                                     (42)

A relatív tömeghiány (A,Z) a vas izotópoknál a legnagyobb (~ 0.786%), és a hidrogénnél is nagyobb mint 10. Nagyobb magtöltéseknél a relatív tömeghiány

|(A,Z)- (A,Z)| < 0.14%,                             Z > 10,

aránylag csak kicsit függ az A-tól. De a legtöbb kémiai elemnél az izotópok tehetetlen tömege közel 0.75%-kal különbözik a gravitációs tömegtől. Ez aláhúzza Einstein Ekvivalencia Elvének az érvénytelenségét az egyesített mező elméletben.

Ha a Nukleáris Táblázatokból [10] vesszük az adatokat a tömeghiány kiszámításához, akkor ügyelni kell, mert ott a semleges izotópokra vannak a mért tömegek megadva. A mérés sokszor pozitív töltött izotópokkal történik és az elektron tömege hozzá van adva a megmért nyugvó tehetetlen tömeghez

m(A,Z) = A( m+ m) + 2 N(e,p ) m(e)– E/c.

Itt az N(e,p) a mageröt okozó -neutrínók számát adja meg az atommagban. Összevetve a (42)-vel megkapjuk a relatív tömeghiány és a kötési energia összefüggését.

(A, Z) = E/c - 2 (A + N(e,p)) m

 

Hátra maradt még a h meghatározása. Mivel más lehetőség nem állt fenn számomra, felírtam a Planck állandót a H-atomnál olyan formában, hogy abból a h-t is ki tudjam számolni. Miért tudok analóg kifejezéseket a H-atomra és a neutrínókra felhasználni? Azért, mert az alapvető kovariáns Hamilton elv a H-atomnál és a neutrínóknál csak a fellépő gravitációs tömegekben különbözik. Az ionizációs energiát E meg azért használhatom, mert ez az energia a h és a h által képezett alapállapothoz tartozik. Az alapállapotoknál a Lagrange multiplikátorokból az E kiszámítható és az E/c  összehasonlítható a redukált tömeggel.

A Planck állandó célravezető feírása a H-atomnál

h = q/(2c) = q/2c x (m’c/2E),                        (43)

ahol az E=13.59 eV az ionizációs energiát és m’ = mm/(m+m) a redukált tömeget adja meg. A neutrínóknál az ionizációs energiáknak

a)   E  = 2 m c ,      b)   E  = 2 m c ,           (44)

vettem. Ezeket és a redukált tömegeket,

a)   m’ = m/2,                       b)   m’ = m/2,                           (45)

behelyettesítve a (43) jobboldalába, és a két neutrínóra

h = q/2c x 1/,                                                                  (46)

ugyanazt az értéket kaptam ki. A h-ban az összetevő részecskék tömege kiesett. A (43) és (46) egyenletek után a fundamentális állandó h = h/387.7 sokkal kisebb, mint a Planck állandó. Mivel A. Sommerfeld (1868-1951) megadása (43) után az  a H-atomban az elektronok sebességét c egységben mérve adja meg, a részecskék sebessége a neutrínókban (46) erősen relativisztikus: v/(c-v) =v/c = /3 = 94.28% .

Egy analóg összefüggést használok fel a H-atom sugarából is

r = h/(qm’),                                                                   (47).

a neutrínók nagyságának a meghatározására. Ebből az elektronneutínónál, (45a) után

r= h/(qm’) = 7.03x10cm,                                         (48)

a protonneutrínónál pedig, (45b) után

r = 3.83x10cm -t                                                                (49)

kaptam. A neutrínók átmérője megfelelt a két felépítő részecske relatív távolságának, egy kör alakú pályán. Az atommag, kiszámítva a H-atom d = 2xr átmérőjével, kb. r/d = 0.66x10-szer, kisebbek mint az atomhéj, ami megfelel a megfigyeléseknek az atommagok nagyságáról.

A Hamilton elvből (14) kiinduló variációs számítások a mag modellezésre, a stabil magokra éppúgy, mint a radioaktív magokra, felhasználhatók. Ezekből a h segítségével kiszámíthatjuk a kötési energiát, az instabil magoknál az élettartamot, az elektronneutínók számát M(A,Z) és a töltések eloszlását a magokban. A (,e)-kötésekre a modellezésnél irányt mutatók a részecskefizikából nyerhető ismeretek.

Ezzel véget is ért az atommagokra tervezett áttekintésem. Fontos megjegyezni, hogy az elektron és a pozitron fellépnek a mag összetételében és az elektronneutínók képezik a h közvetítésével a magerőt. A magban a (,e) képződménynek egy összekötő szerep jut a protonok között. Ez magyarázatot ad a fenomenologikusan észlelt magerő tulajdonságaira, arra tehát, hogy a nukleonok nem szeretnek egymáshoz nagyon közel kerülni, a magerők telítődnek és hatótávolságuk 1 fm = 10cm nagyságrendben van. A felsorolt megfigyelések alátámasztják, hogy az egyesített mező elmélettel a magoknál is jó úton járunk.

 

Az egyesített mező elmélet a részecskefizikában

Sokan megkérdeztek, hogy mivel magyarázom az ún. gyenge- és erős-kölcsönhatást, ha csak az egyesített mező létezik a természetben? A válasznál mind a kétfajta neutrínó  és  ismerete és a h fontos szerepet tölt be. Mellékesen jegyezzük meg, a szabad neutrínók nem fénysebességgel (amit néhány kutató feltételez) mozognak, mert a neutrínók tömeget hordozó részecskékből állnak. (Az SN 1987a szupernóva felvillanásával detektáltak néhány neutrínót, ezek csak megközelítően mozoghattak fénysebességgel.) Mint már megismertük, a kiszámolt átmérők, r= 0.73x10 cm, r= 3.836x10 cm, az mutatják, hogy a magerőknél csak az elektronneutrínó  játszik szerepet. Ez megfelel annak a megfigyelésnek is, hogy a kísérletekben a magok bomlásánál soha nem látjuk az eltont, a protonneutrínó  egyik összetevőjét, megjelenni. Az elton és a  az ún. erőskölcsönhatás magyarázatánál és a szupernóva robbanásoknál tölt fontos szerepet be. A neutron és a magok -bomlásánál fellépő elektron és pozitron, a  kíséretében, új feltevés nélkül megérthetővé vált, mert ezek megtalálhatók az instabil neutronban és magban. Ezek a bomlások képezik összefogóan az ún. gyengekölcsönhatást a részecskefizikában.

Most az ismertebb “instabil részecskék” felépítését ismertetem. A stabil neutron szerkezetét, mint az elektron és a proton kötött állapotát, N = (e,P), már említettem. A magokat

N = (P, 2e, p) = P + e + ,                                            (50)

is elhagyhatja, amit “mag-neutronoknak” is lehetne keresztelni. A kísérletek csak az N-t figyelték meg, így a fizikusok az hiszik, hogy csak ez létezik. Az N  bomlásánál azonban vigyázni kell a „sötét anyag” jelenlétére is, mert nem tudni, hogy egy szabadon mozgó N nem találkozik-e egy -vel, ami után a bomlás (50) történik. Mindenesetre a stabil N tehetetlen tömege kisebb, a N-nek pedig nagyobb, mint a proton tömege m és valószínűen kisebb ill. nagyobb mint m-m.

Az instabil müon (S. H. Neddermeyer, C. D. Anderson felfedeztése 1938-ban) bomlásában észlelt részecskék

  e +  + ,         p +  + ,                        (51)

a müon szerkezetét nyilvánítják ki. A müon, amely élettartama  = 2.2x10s a legnagyobb az összes instabil mezon féle részecskék között, öt elemi részecskéből áll

 = (P, 2e, p, E),  = (P, e, 2p, E).                                       (52)

Az instabil részecskéknél bizonyos fokig megmutatkozik az összetevő részecskék gravitációs tömege a részecskék nyugalmi tehetetlen tömegében. Hasonló jelenséget már az atommagoknál megismertünk, de ott tömeghiány van, ami nem haladja meg az egy százalékot. Az instabil részecskéknél „tömegtöbblet”-ről kell beszámolni és ez valamivel nagyobb effektus. A negatív müon gravitációs töltése akkora, mint az elektroné, de a tehetetlen tömege 207-szerese az elektron tömegének. A müon tehetetlen tömegénél a P-nek és az E-nek a 2m tömege már 5.6%-ban észlelhető. A részecskefizika nem tudja mérni a gravitációs tömeget, a nagyon gyenge gravitációs erő miatt, az itt észlelt tömeg csak a tehetetlen tömeg. A tehetetlen tömegmegmaradását a részecskefizikában soha nem szabad úgy tekinteni, mint egy megmaradási törvényt. A gravitációs kölcsönhatást, az erő gyengesége miatt a részecskefizika, éppúgy, mint a magfizika, teljesen elhanyagolja. Ez az erő nagysága miatt megérthető, de mégis hiba volt, mert a gravitációs tömeg, mint az invariáns gravitációs töltés leszármazottja, soha nem változik meg a reakciókban. Az elektromos és a gravitációs töltések állandósága adja az egyetlen megmaradási törvényt a részecske reakciókban.

Mivel az instabil müon tömege 207-szor nagyobb mint az elektroné, az atomok által befogott müon közelebb kerül az atommaghoz mint az e, és protonneutrínó kibocsátása mellett, segít beépíteni a magba egy e-t, p-t vagy egy -t. Ez a reakció, a neutron befogása és a  közvetlen belépése mellett, építi a magokat. A protont és a pozitront a pozitív e-töltés taszítja ki, az elektronokat meg normális körülmények között a Planck állandó fellépése nem engedi be a magba.

Az instabil pion (C. F. Powell felfedezése 1947-ben) bomlásából

   + ,                                                                    (53)

viszont az következik, az elfogadott elképzelésekkel ellentétben, hogy a pion semmi szerepet nem játszik a magokban, mert a szerkezete egy eltont is tartalmaz. A két töltött és a semleges pion szerkezete, feltételezve, hogy a (53) bomlásnál csak egy  szerepel,

 = {,,} = {(P,3e,2p,E), (P,2e,3p,E), (P,2e,2p,E)}. (54)

A  tömege 280-szor, viszont a  csak 270-szer, nagyobb mint az elektron tömege. Továbbá feltűnő, hogy a töltött pionok megfigyelt élettartama = 2.6x10 s sokkal nagyobb, mint a  „élettartama” 0.8x10 s. A semleges pion feltételezett szerkezete,

 = (P,2e,2p,E),                                                                   (54’)

abban különbözik a töltött pionokétól, hogy ott még egy e vagy p is szerepel. De a  nem semmisülhet meg elektromágneses hullámok kibocsátása után. A szakirodalomban megadott híres reakció

 2,         nem létezik                                                      (55)

a természetben. A  szerkezete egy többlet -vel különbözik a  = (P,,E)-tól. A részecskefizának nem sikerült megfigyelni kísérletekben azt, hogy a  stabil marad, vagy szétesik

 + ,             +  +  ,                      (55’)

mert ezeket a bomlásokat eddig még nem lehetett észlelni.

A töltött „instabil részecskék” szerkezetében van, a semleges és tömegnélküli (e,p), (P,E)-párok mellett, legalább még egy töltött részecske. A szerkezetük felismerésénél felhasználom a (P,,E), (P,,e,P) és (E,,p,E) kötési formákat. Az instabil részecskék szerkezetének a modellezésénél is a Hamilton elvből kiinduló variációs számítások fognak segíteni. Először a „sötét anyag” stabil összetevőit kell megtalálni, az

Nx(e,p)+Mx(P,E)   {ezek szerintem a „sötét anyag” elemei}       (56)

szerkezetű képződmények között. A „sötét anyag” tulajdonsága, a mai asztrofizikának az egyik alapvető rejtélye, így kiszámíthatóvá vált. Az asztrofizikai modellek szerint az Univerzum teljes anyagát, ill. energiáját, 75%-tól  95%-ig a „sötét anyag” teszi ki. De a „sötét anyag” csillagok körüli eloszlásáról nem tudunk sokat. Valószínűnek tartom, hogy a 100 MeV feletti részecske-reakciókat a „sötét anyag” dominálja. A részecskereakciókban a négy elemi részecske száma mindig megmarad, de a „sötét anyagból” származó semleges és tömegnélküli (56) szerkezetű képződmények fellépésével mindig számolni kell.

A mezonok szerkezetében mindig egyenlő számú proton és elton van. Az itt felmutatott út az „instabil részecskék” új rendszerbe való besorolását írja elő. A kaonok szerkezetét a bomlásokból értelmezni már azért bonyolultabb, mert a négy elemi részecske tükrében, az „instabil részecskék” eddigi rendszerezése nem egyértelmű. Az eddigi rendszerezés hiányossága a töltött kaonoknál már megmutatkozik. A K, K bomlásainál én abból indulok ki, hogy a részecske szerkezetekben további -k és legalább két  jelen van.

Kísérletekben a

K = (2P,2e,3p,2E)+ ,        63%,                             (57)

bomlás a leggyakoribb, de van több pionra bomló kaon is

K = (2P,4e,5p,2E) + ,         22%,                         (57’)

K = (3P,6e,7p,3E) ++.    5,6%.                      (57’’)

Az sincs kizárva az sem, hogy például a (57’) bomlásnál a K = (2P,2e,3p,2E) egy (,) képződményt kölcsönöz ki  a „sötét anyagból” és azután keletkezik a két pion.

K bomlások gyakrabban megfigyelhetők mint a hasonló K bomlások, így például a

K = (2P,3e,2p,2E)+ .                                             (58)

A kaonok tömege több mint 986-szorosa az e tömegének így (57) után a felépítő gravitációs tömegek 13%-a látható meg a kaonok tehetetlen tömegében. A töltött kaonok élettartama 1.24x10 s. A semleges kaonnak két különböző élettartama van, 5x10 s és 1x10 s, aminek a magyarázata a részecskefizikában még máig sem kielégítő. A semleges kaon lehet (2P,3e,3p,2E) vagy (2P,4e,4p,2E) szerkezetű is. Általában a semleges instabil részecskék (, K, , , ) szerkezetét mindig nehezebb rendszerezni, mint a töltött részecskékét, a -k ismeretlen száma miatt .

A barionok szerkezeténél megfigyelhető, hogy a protonnak és az eltonnak a száma mindig eggyel különbözik. A barionokból csak egy-két egyszerűbb szerkezetet említek meg, de elöre utalok a semleges instabil részecskék osztályzásának a bizonytalaságára:

 = {(2P,3e,2p,E)  vagy (P,2e,3p,2E)},                                (59)

 = {,,} =
{(2P,2e,2p,E),(P,2e,2p,2E), (2P,4e,3p,E) és (P,3e,4p,2E)},
                                                                                                  (60)

 = {,,}=
{(3P,4e,4p,2E),(2P,4e,4p,3E),(3P,5e,4p,2E)/(2P,4e,5p,3E)}. (61)

A  és a   részecskéknél is, az elektromos töltésüktől függően, a tehetetlen tömeg és az élettartam egy kicsit különbözik.

Az ún. barion erőskölcsönhatásnál meg kell különböztetni, a Standard Modellben (SM) mint a ritkaságot (strangeness) nem változtató reakcióknak elnevezetteket, pl.

P + P  + D,             + D P + P,                            (62)

a ritkaságot változtatóktól, pl.

 + P  + K,           + P  + K.                           (63)

Az első reakcióban hozzávetőleg egy  a másodikban két vagy több  is felléphet, számos kíséretében, kikölcsönözve a „sötét anyagból” ami körülveszi a reakció partnereket. Ezért én úgy értelmezem a SM ún. erőskölcsönhatását, hogy a „sötét anyagból” részecskepárok, különösen -k, lesznek kikölcsönözve, ill. leadva. Viszont a magokban ezt nem látom. A Standard Modellben gyakran idézett erőskölcsönhatást sem, mert a magokban az elton és a  nem léphet fel.

A „sötét anyag” jelenléte a „részecskeképzésnél” is fontos. A „részecskeképzés” szerintem megfelel a  és -neutrínók szétválasztásának a (e + p) és (P + E)-párokra, egy elegendő nagy rezgésszámú elektromágneses hullám hatásánál. Innen megérthető, hogy az „anti-részecske” kifejezést az egyesített mező elméletben mellőzöm.

A felrajzolt „instabil részecske” szerkezetekből kiindulva, sok eddig megmagyarázatlan tény felé „kinyílott egy ajtó”, új alapvető ad hoc feltevések nélkül. Nincs szükség az ún. gyenge- és erőskölcsönhatás bevezetésére sem, mint új fundamentális mikroszkópikus kölcsönhatásokra. Továbbá, nincs szükség a quark-féle alapvető részecskékre és a húr-/membrán-féle konsztruktok bevezetésére sem egy többdimenziós térben. A fizikai térnek Minkowski metrikje van, amiben a mezők és a részecskék propagálnak. Az egyesített mező elméletnél elég a négy stabil részecske (e, p, P és E), a kétfajta elemi töltéssel és az általuk okozott két alapvető kölcsönhatással. Az „instabil részecskék” nyugalmi tehetetlen tömegét, élettartamát és szerkezetét a Hamilton elvből (14) variációs számítások adják ki.

Konklúzió: Az egyesített nem-konzervatív mezőknél az energia kvantálás, mint sajátérték probléma, nem léphet fel, a mikroszkópikus fizikában sem. A Planck állandó, h, a Minkowski tér egy Lagrange multiplikátorából származik, ezért a kvantummechanika formalizmusát egészében újra kell értelmezni. A Planck állandó mellett még egy fundamentális állandót, a h-t, találtam. A h-n keresztül a  elektonneutrínó határozza meg a magerőt. Az általunk ismert magok a három elemi részecskéből (e, p és P) vannak felépítve. Az izotópok gravitácós tömege csak a tömegszámtól függ. Az anyag tehetetlen tömege viszont különbözik a gravitációs tömegétől amit, ismert összetétel mellett, az izotópok tömeghiánya megad. Az instabil részecskék szerkezete tartalmazza a  = (P,E) protonneutrínót is. A részecskereakciókban 100 MeV felett megmutatkozik a “sötét anyag”. A “sötét anyag” a kétfajta neutrínó és a hozzájuk hasonló semleges és tömegnélküli képződményekből áll. Az új elmélet, az egyesített két alapvető kölcsönhatással és a kovariáns Lagrange formalizmusban betelepített Hamilton elv felhasználásával, egy egyszerű és konzisztens leírását ad a mikro- és makrokozmosznak. Az alapvető problémák a jelenlevő nem-konzervatív rendszereknél, nagyrészt megoldottak [7, 8, 9]. A bemutatott egyesített mező elmélet teljes egészében megfelel a sokat keresett Nagy Egyesített Elmélet (UFT = Unified Field Theory) feltételeinek és matematikailag is konzisztensnek mutatkozik: az elméletben felvett hipotézisek megegyeznek a mezők tulajdonságaival és a mezőegyenletek a Hamilton elvből levezettett Lagrange egyenleteknek tekinthetők, a mezők Lorentz feltélei mellett. Az egyesített mező elmélet csak invariánsokat, elemi töltéseket és az egyesített mező véges terjedési sebességét, és a Lagrange multiplikátorokat ismer, mint állandókat. Az elmélet nem használ se nem helytálló általánosításokat, se nem támaszkodik matematikailag ugyan lehetséges, de kísérletek magyarázatához szükségtelen formalizmusokra.

 

Idézetek:

[1]     Gravitation: Urkraft des Kosmos, Sterne und Weltraum, Special Heft 6, (Mai 2001), Ez egy összeállítás az Albert Einstein Intézet, Potsdam, kutatói vezetése alatt;  Kosmologie, Spektrum der Wissenschaft, Dossier 3 (2004);  Jenseits vom Raum und Zeit: NATURGESETZE. Was die Welt zusammenhält, Bild der Wissenschaft, Heft 12, (2003).

[2]     M. Born, Die Relativitätstheorie Einsteins, 5. Auflage, Heidelberger Taschenbücher, Springer, Berlin-Heidelberg- New York (1969); C. Will, Theory and experiment in gravitational physics, Revised Edition (Cambridge University Press, Cambridge, 1993), R. H. Dicke, The theoretical significance of experimental relativity, (Gordon and Breach, NY-London-Paris 1968).

[3]     M. Giaquinta, Stefan Hildebrandt, Calculus of Variations I (Springer-Verlag Berlin, Heidelberg 2004), lásd Chapter I.2.

[4]     Gy. I. Szász, Z. Phys., A275, 403 (1975); Z. Phys. A278, 165 (1976); Fortschr. d. Physik, 24, 405 (1976); Phy. Lett. A55, 327 (1976); Phy. Lett. A62, 313 (1977).

[5]     V. Marigliano Ramaglia, G.P. Zucchelli, Phy. Lett. A67, 9 (1978).

[6]     G. Källén, Elementarteichenphysik, (Hochschultaschenbücher, BI Bd 100, Mannheim, 1964), J. D. Bjorken, S. D. Drell, Relativisische Quantenfeldtheorie, (Hochschultaschenbücher, BI Bd 101, Mannheim, 1965); Kiss D., Horváth A., Kiss Á, Kísérleti Atomfizika (ELTE Eötvös kiadó, Budapest 1998).

A szerzőnek a témához tartozó, még meg nem jelent dolgozatai amik itt fejezetekben vannak bemutatva:

[7]     Emission of Radiation by Atoms without the Energy Quantum Hypothesis, (2002);

          Principles of Physics, (2003);

Model of the Unified Field and the Neutrinos, (2003);

Treatment of the Fundamental Field with Calculus of Variation, (2004).

 [8]    The Non-Equivalence of the Inertial and Gravitational Mass within a Theory of Gravitational Charges, (2002);

          The Orbits of Planets Violate the UFF, (2003);

          Measurement of UFF Violation with Li/C/Pb Compared with AL, (2004).

[9]     Mi okozza a gravitációt? (What causes the gravity?) (2004)

 

[10]   G.Audi, A.H.Wapsta, Nuclear Physics, A598, 409 (1995).

[11]   Gong BinXin, The Classical Electrodynamics Approach to Explain the Photoelectric Effect, http://www.wbabin.net/physics/xin2.pdf.